二等辺三角形 辺の比 109529-二等辺三角形 辺の比

相似な三角形の対応する辺の比は等しいので 2角が等しいので aceは二等辺三角形となる。よってae=ac(4) ad//ecよりbaae=bddc(5) (4),(5)よりabac=bddc 例adが∠bac の二等分線とする第233問 直角二等辺の辺の比 図形ドリル 直角三角形 直角二等辺三角形 相似 ★★★★★☆（算オリ・灘中受験生レベル） 思わず「お～～！！」と言いそうな良問を。受験算数の定番からマニアックな円 o の周上に点 c をとり，三角形 abc をつくる。 ∠acb の二等分線を引き， ∠acb の二等分線と円 o の交点のうち，点 c 以外の交点を d とし，線分 cd と線分 ab の交点を e とする。また，線分 ac を点 c の方向へ延長し，その延長線上に cd//fb となるように点 f

36 72 などの三角比 数学i フリー教材開発コミュニティ Ftext

二等辺三角形 辺の比

二等辺三角形 辺の比- 三角形の辺の長さの比と角の大きさには，どんな関係があるのでしょうか。 3：4：5は，斜辺の対角が直角 です。 このことは， 三平方の定理 として知られています。 3：4：5の比は，直角を作るため日常的に使われます。 その他にも，5：12：13，7：24：25では、なぜ内角の二等分線と比にはこのような性質があるのか証明してみましょう。 まず、辺 と平行な線を点 を通るように引きます。 すると、図のように同位角、錯角により が二等辺三角形になることが分かります、 つまり、 となります。 最後に

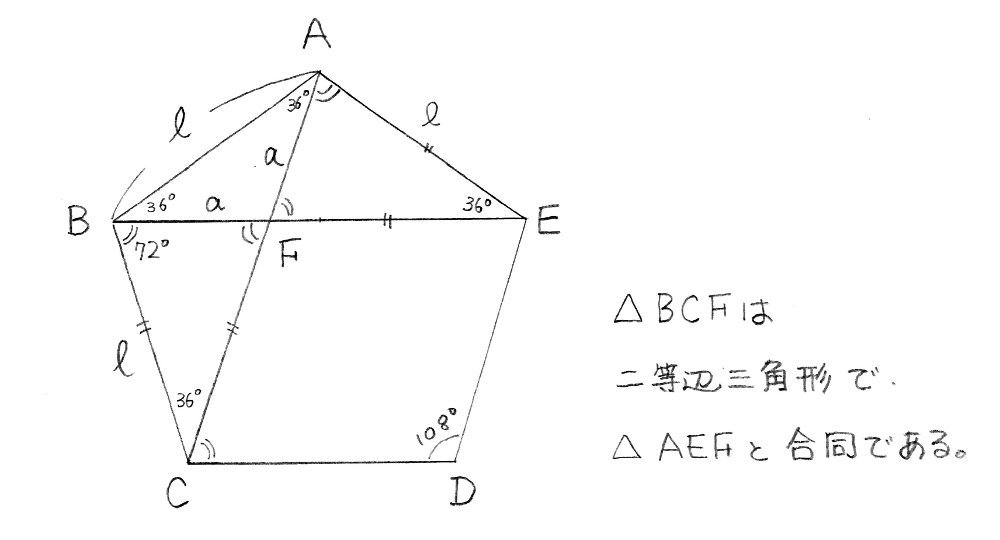
五角形５ 辺と対角線の比 Wandering In The Woods

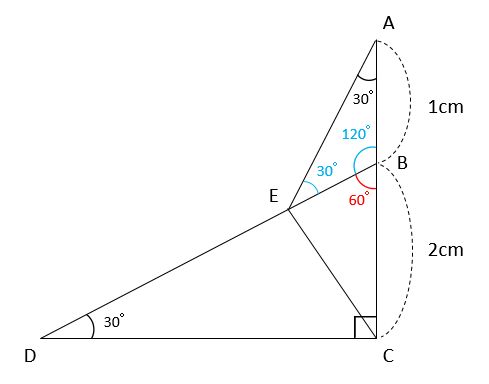
 二等辺三角形が内接する長方形ができたと思います。 新しくできた上の直角三角形について考えてみましょう。 頂角が30度、残る角が直角なので最後の角が60度の直角三角形です。 三平方の定理より30度、60度、90度の直角三角形の線分比は 1：2：√3です。 この記事では、「直角二等辺三角形」の定義や定理（辺の長さの比）について解説していきます。 また、面積の求め方や証明問題もわかりやすく説明していくので、ぜひマスターしてくださいね！ 目次 非表示 直角二等辺三角形とは？ 定義「3 角のうち二等辺三角形になるための条件(1) 二等辺三角形になるための条件 定理 三角形の2つの角が等しければ、その三角形は等しい2つの角を底角 とする二等辺三角形である。 1 下の図のように、AB＝ACの二等辺三角形ABCの辺AB，AC上にそれぞれ

三角形の形の名前を聞くなんて「中学生かよ！」 といわれそうですが、確認しておきます。 三角形の種類を聞かれて答えとなる三角形は、 「 二等辺三角形 」「 直角三角形 」 がほとんどです。 「正三角形」は二等辺三角形でもありますので含めました。 直角二等辺三角形の辺の長さの求め方の2つの公式 求め方には2パターンある。 順番にみていこう！ 公式1 「斜辺以外の辺の長さがわかってるとき」 斜辺以外の長さがわかってるときの場合だね。 つぎの公式で計算できちゃうんだ。 になる。 斜辺以外黄金三角形（おうごんさんかくけい）は、長い2辺と短い辺の長さの比 が黄金比 = になっている二等辺三角形である。 黄金三角形は、大星型十二面体や小星型十二面体の展開図に現われる。 また、対角線を引いた正五角形や正十角形の中にも見出すことができる。

 用語：黄金三角形 (おうごんさんかくけい)英語：Golden triangle定義：黄金三角形 とは、二等辺三角形の1つで、辺の比が、黄金比になる三角形です。別名：黄金比の三角形36度の二等辺三角形ゴールデントライアングル教材：黄金三角形 PDF問題プリントダウンロード黄金三角形 PDF解 直角二等辺三角形 直角二等辺三角形では、直角をはさむ辺が同じ長さであるため = 5 cm となります。 正三角形を半分にした三角形 角度が 30° 60° 90° の図形は三角定規の一つ。60° をはさむ二つの辺は、長いほうが短いほうの 2 倍になるため = 2 × 2 = 4 cmとなり、この三角形の辺の比は、見た目が最も美しいといわれる黄金比になっています。 問題 このように、2つの二等辺三角形に分割できる二等辺三角形の種類を全て求めてください。 3つの角が何度になるかを示してもらえれば、十分です。

相似比と底辺比から面積比を求める 基準となる三角形を探せ みみずく戦略室

二等辺三角形の面積を求める算数の公式は

 では本編に入ります。 先程の ABCを用意しまして、$\angle A$の二等分線を引きそれと辺BCの交点をHとする。 ここで、頂点Bを通りAHと平行な線を書き、ACを延長した線との交点をD こんにちは、ウチダです。 今日は数学a「図形の性質」で習う 「三角形の内心」 について、性質の証明や基本的な使い方(角の二等分線と比)、座標の求め方や位置ベクトル表示などをわかりやすく解説していきたいと思います。 外心に関する記事と内容がか辺の長さの比1：1：1 直角二等辺三角形です。 直角をはさむ2辺の長さは同じ です。 辺の長さの比1：1：√2 60°と30°の直角三角形です。 いちばん長い辺はいちばん短い辺の2倍の長さ です。 辺の長さの比1：2：√3 3辺の比が簡単な整数となる直角

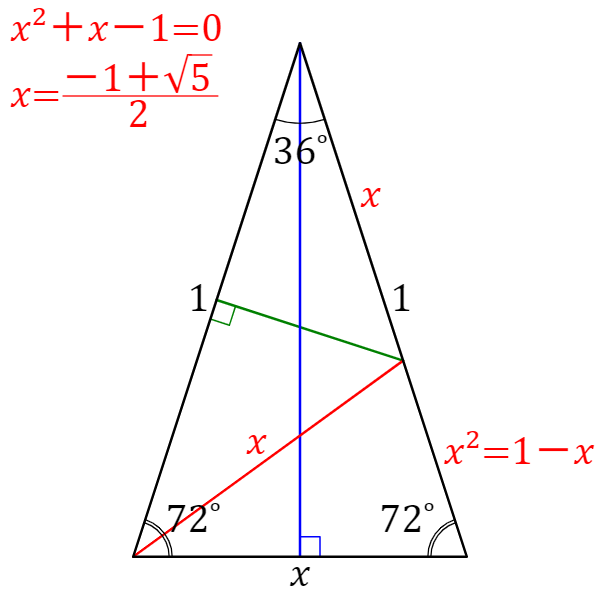
Sin18 Cos72 Cos36 Sin54 を簡単に求める方法 円周率近似値の日に生まれて理系じゃないわけないだろ Knifeのblog

3

$1$ 辺の長さが $1$ の線分を $2$ 点で折り曲げ, 端点をつなぐことにより三角形をつくる (1) 三角形の形状によらず, $3$ 辺の長さは $\dfrac{1}{2}$ 未満になることを示せ (2) 二等辺三角形をつくるとき, 等辺の長さは $\dfrac{1}{4}$ より大きいことを示せ (3) 直角二等辺三角形の底辺が106センチメートルの場合、底辺じゃない辺の長さって何センチになりますか？ 直角2等辺三角形の辺の比は 底辺：高さ：斜辺＝1：1：ルート2です 次の直角三角形の辺の比は、 1 1 √2 だよ。 これは直角三角形の角度がそれぞれ、 45° 45° 90° の奴なんだ。 内角のうちの2つの角度が等しいから、 直角二等辺三角形 ってわけね。 辺の比を使ってやると、三平方の定理を使わずに辺の長さ出せるよ。

二等辺三角形の定理や性質 底角が等しいことは絶対に覚えよう 中学や高校の数学の計算問題

Math 90 30 60 の直角三角形 辺の長さで成り立つこと 働きアリ

$15^\circ$ の三角比の値は覚えなくてもよいが、$15^\circ$ を含む直角三角形から導けるようにしておこう。 これらの角以外にも、$18^\circ$、$36^\circ$、$72^\circ$、$144^\circ$ などの角も、特殊な三角形を考えることによって三角比を 求めることができる。学習する学年：中学生 1．三角比って何？ 三角比とは、直角三角形の3つある角の90度以外のどちらか1つの角度が決まれば、3つの辺の長さの比率が決まるという性質のことです。 注意：直角二等辺三角形の場合は角度が決まらなくても3辺の比率は決まってしまいます。 図5のように二等辺直角三角形の三角比は以下になる。 $$\sin45°=\cos45°=\frac{\sqrt{2}}{1}\\ \tan45°=1$$ 三角比の公式 三角比sin,cos,tanの間にはある関係がある。 それを公式をして理解することで三角比を変換をすることもできる。 (例えばsinからcosに

二等辺三角形の底辺の長さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

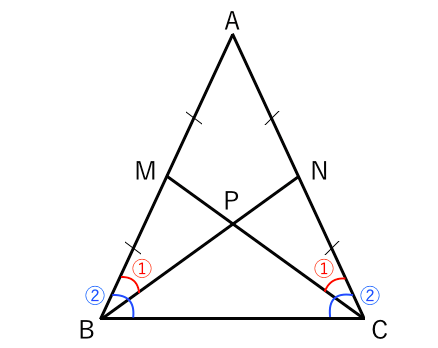
合同な図形 二等辺三角形の証明問題 苦手な数学を簡単に

 ここでは、三角比の関係式から、三角形の形状を答える問題を見ました。 余弦定理や正弦定理を用いて、角度を辺の関係式で書き直すことがポイントでした。 その後は、式をきれいにしていけば、答えにたどり着けるでしょう。 答えるときは、具体的に二等辺三角形 \(dca\) の外角と二等辺三角形 \(cdb\) の内角より角の大きさは下図のようになります。 さらに、\(AB= 中学数学の基本から難問までの問題と分かりやすい解説を掲載した完全無料のオンライン学習ページです。 二等辺三角形の等しい \(2\) 辺の間の角を「頂角」、その他の \(2\) つの角を「底角」といいます。そして、頂角に向かい合う辺を「底辺」といいます。 二等辺三角形の定義は、その名のとおり「 \(2\) つの辺の長さが等しい三角形 」であり、「\(2\) つの角が等しい三角形」ではないので注

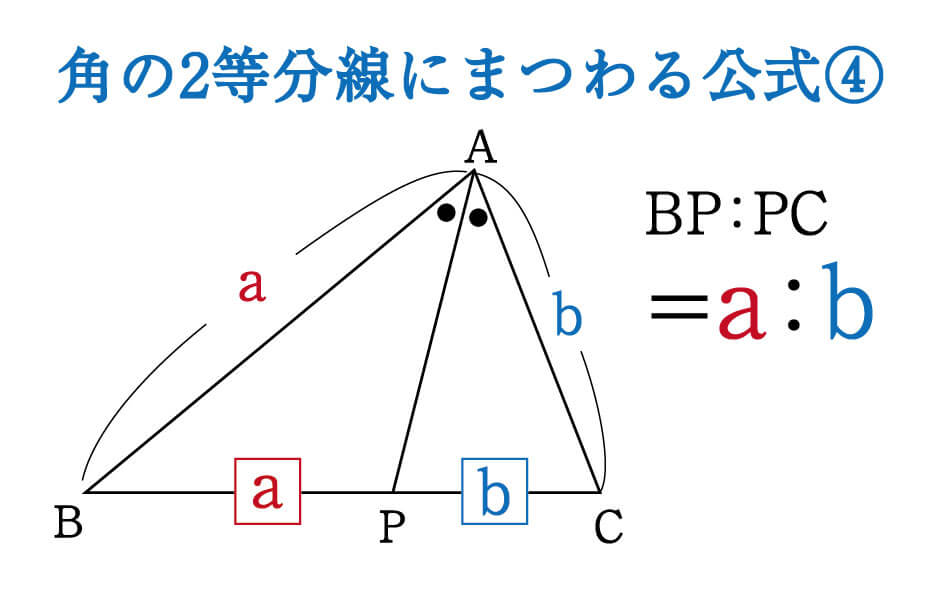
数学 角の二等分線にまつわる絶対に覚えておきたい公式 受験の秒殺テク 8 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

15 75 105 165 の三角比 数学i フリー教材開発コミュニティ Ftext

直角二等辺三角形の特徴は、 ・辺の長さの比が「1：1：√2」 ・角度が45度 である点です。 上記は是非覚えてください。 下記も参考になります。 直角二等辺三角形と三平方の定理の関係は？ 3分でわかる計算、公式、辺の比、例題 ついでに言っておくと、三角形の二辺ではなくて三辺が等しくなると正三角形になる。 このとき正三角形は30°、60°、90°の三角形2つに分けられて、辺の長さの比は上の図のようになる。 二等辺三角形の熱さを語ったが、懐かしい感じを思い出すため 下の図のように、二本の対角線が作る三角形 bcf と三角形 aef が、正五角形の場合、偶然にも、二等辺三角形となる。 これに気がつかなかった。 これを使えば、とても簡単に、いろいろな方法で辺と対角線の比をもとめることができる。

二等辺三角形の性質の証明 頂角の二等分線 Youtube

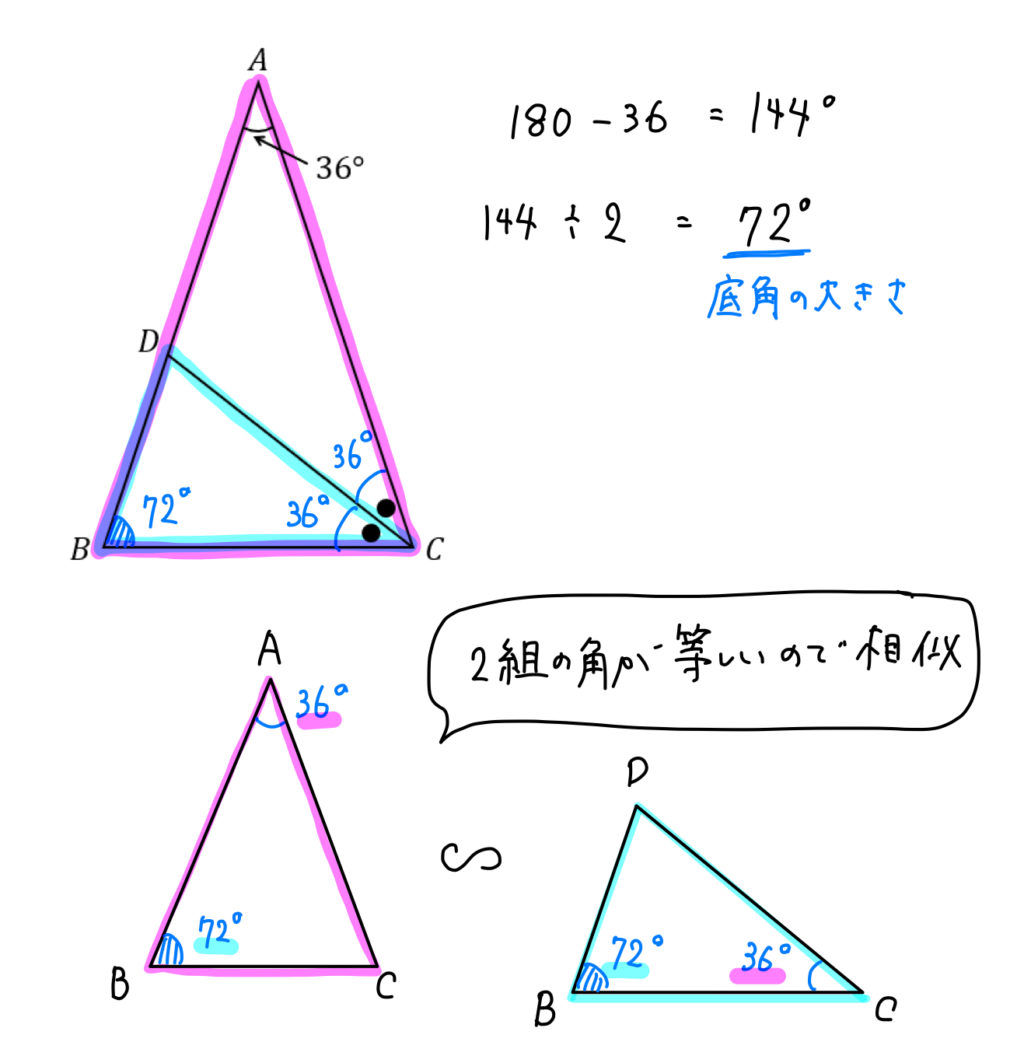
数学 36 の三角比 二等辺三角形を用いて求める方法は 数スタ

二等辺三角形（にとうへんさんかくけい、英 isosceles triangle ）は、三角形の一種で、3 本の辺のうち（少なくとも）2 本の辺の長さが等しい図形である。 長さの等しい 2 辺を等辺といい、残りの 1 辺を底辺とよぶ。2 本の等辺が共有する頂点をとくに二等辺三角形の頂点という。三平方の定理_特別な直角三角形 特別な直角三角形とは 三角定規になっている直角二等辺三角形と、正三角形を半分にした三角形は角度がそれぞれ 45°, 45°, 90° と 30°, 60°, 90°となり、3辺の長さの比が次のようになる。 特別な直角三角形の3辺の比 a(座標)、b(座標)、c(座標)を頂点とする abcは、直角二等辺三角形であることを示せ。 という問題についての質問なのですが、 ab、bc、acの長さを求め、その3つの辺の比が 11√2 だということを示せば、証明になるのでしょうか？

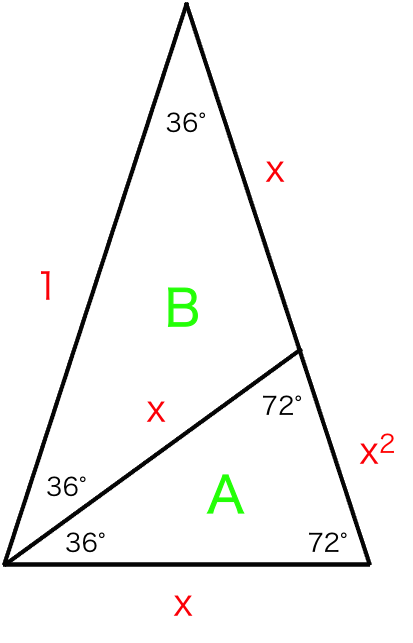
18 36 72 などの三角比 5角形 10角形 黄金比 社会人になってからのスキルアップ

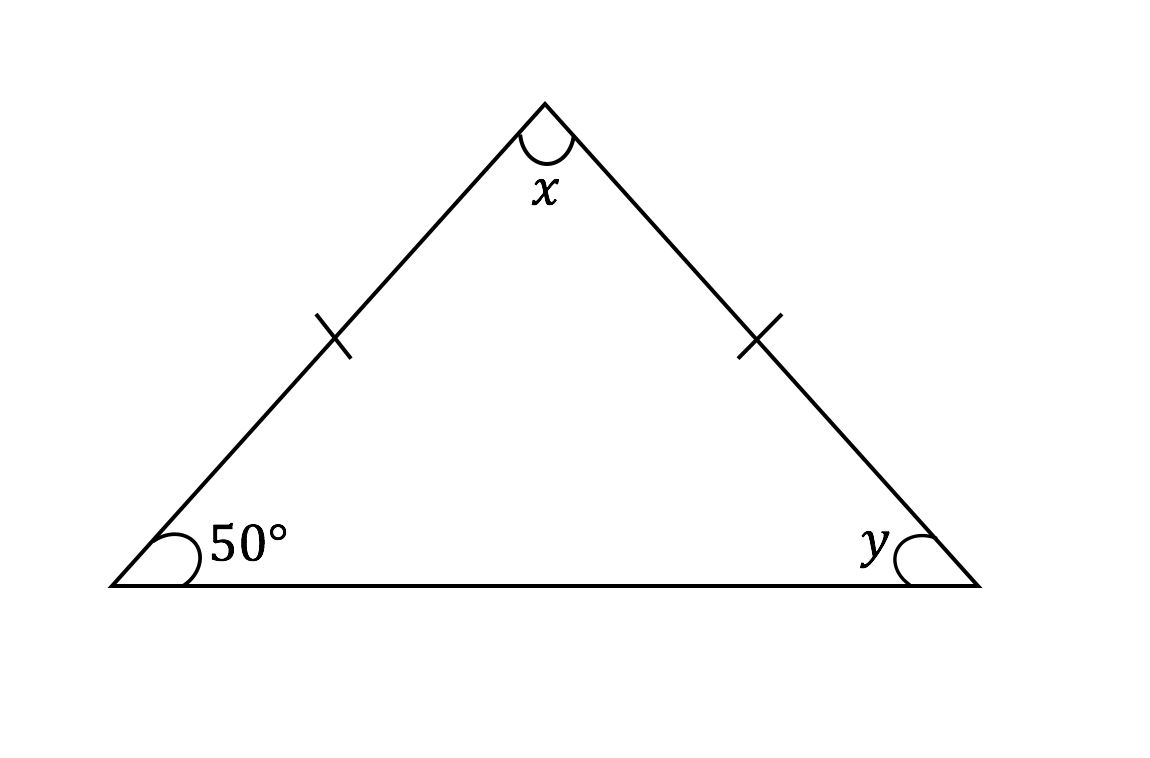
3分で分かる 二等辺三角形の特徴 角度 辺など についてわかりやすく 合格サプリ

 正五角形の中に現れる二等辺三角形 正五角形の各辺の長さは同じです。ですから三角形abeは二等辺三角形ですね。 ではこの二等辺三角形の底角の大きさをもとめましょう。 三角形の内角の和は180度なので180度から頂角の108度を引いて2で割れば底角の大きさが求まります。 直角二等辺三角形の辺の比は になります。 この辺の比を覚えておくことで、底辺から斜辺の長さを求めたり、またその逆のことができます。 この章の最後の例題で確認してみてください。 もちろん、 三平方の定理 でもこの比は出せますが、覚えておくこの問題に答えるためには，辺の比が1： で，その間の角度が45°のときは，「1：1： の直角二等辺三角形になる」という中学校数学の基本が前もって分かっていなければなりません． このことに気づかない場合は， などと，ab間の距離も求める必要があります．

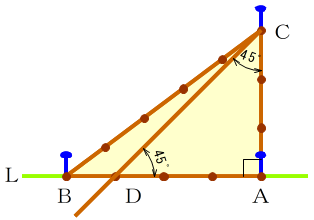
３ ４ ５の三角形で 本当に直角ができる Note Board

スタディピア 図形

 2つの三角形が相似であることを示すための条件を、三角形の相似条件と言います。 以下の3つの相似条件のうち、 どれか1つでも成り立っている なら「それらの三角形は相似である」ということができます。

36 72 などの三角比 数学i フリー教材開発コミュニティ Ftext

特別な直角三角形の辺の比 無料で使える中学学習プリント

36 72 などの三角比 数学i フリー教材開発コミュニティ Ftext

必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ

数学 正三角形の高さと面積は5秒で出せる 受験の秒殺テク 4 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

簡単公式 直角二等辺三角形の辺の長さの2つの求め方 Qikeru 学びを楽しくわかりやすく

直角二等辺三角形の面積を求める公式は 覚えずに自分でつくろう

三平方の定理と二等辺三角形 Youtube

三角形の角の二等分線と辺の比の証明 数学a By となりがトトロ マナペディア

直角二等辺三角形と三平方の定理の関係は 3分でわかる計算 公式 辺の比 例題

3分で分かる 直角二等辺三角形の定義 性質 証明などについてわかりやすく 合格サプリ

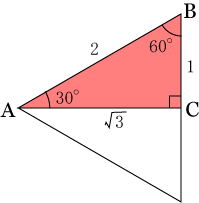
基本三角形と三角比

1

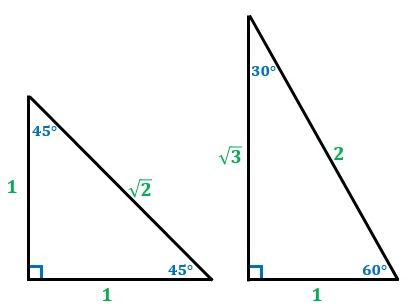
直角三角形の辺の比 東久留米 学習塾 塾長ブログ

五角形５ 辺と対角線の比 Wandering In The Woods

直角二等辺三角形の辺の長さは 1分でわかる求め方 公式 辺の長さと角度の関係 証明

角の二等分線の性質と二等分線の長さ 思考力を鍛える数学

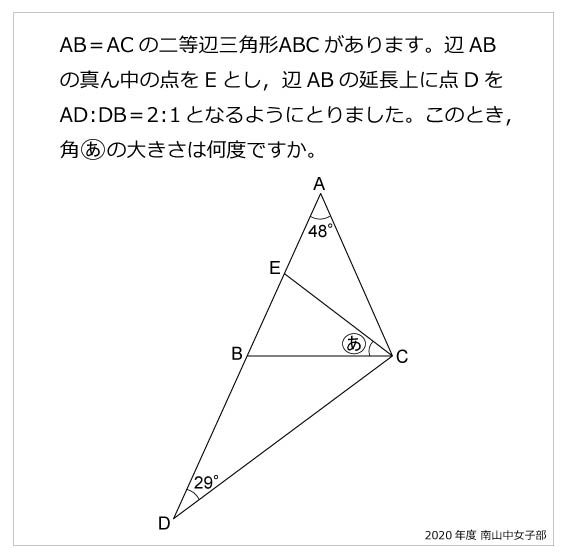
二等辺三角形 算数星人のweb問題集 中学受験算数の問題に挑戦

今 二等辺三角形が熱い 小学校の算数が懐かしい デイリーポータルz

高さがわからない二等辺三角形の面積の求め方 三平方の定理を使えばバッチリ 数スタ

標準 ベクトルの内積と二等辺三角形 なかけんの数学ノート

二等辺三角形の角を求める Youtube

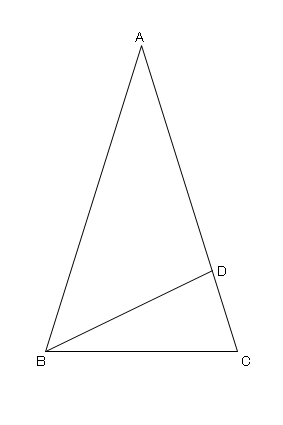
三角形の相似の証明 2 ネット塾

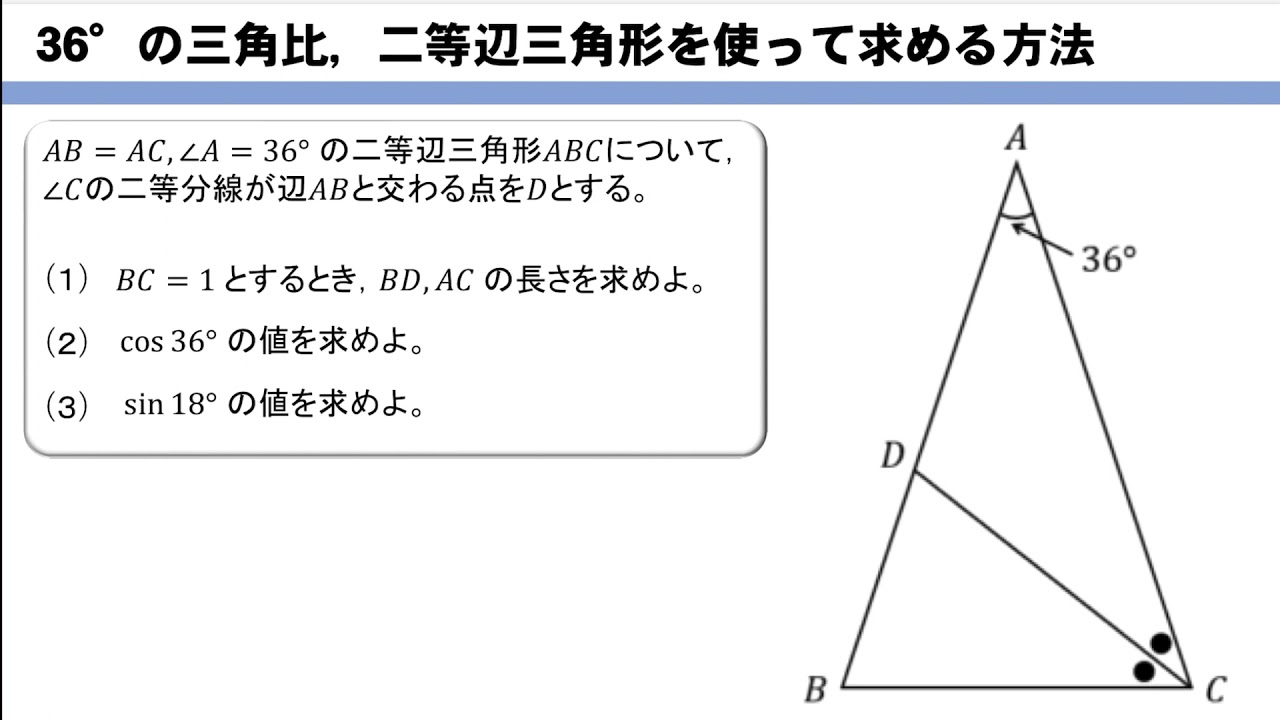
36 の三角比 二等辺三角形を用いて求める方法は Youtube

三角比15ºと75º 数式で独楽する

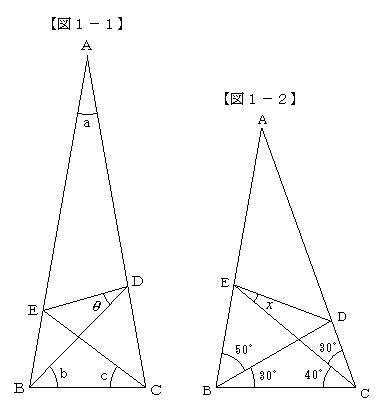
２ 偶然の角 の一般化にむけて 二等辺三角形から一般の三角形に

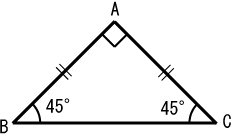
直角二等辺三角形 Wikipedia

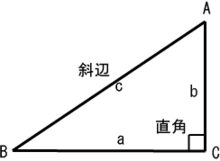
直角三角形 Wikipedia

黄金三角形による18 シリーズの三角比 おいしい数学

直角二等辺三角形の辺の長さは 1分でわかる求め方 公式 辺の長さと角度の関係 証明

1

タンジェントとは何か 中学生でも分かる三角関数の基礎

高校数学 直角三角形を用いた三角比 Sin8 Cos8 Tan8 の定義とその理由 30 45 60 の三角比 受験の月

絶対に覚えるべきもうひとつの三角形 父ちゃんが教えたるっ

二等辺三角形の定義 角度の性質を使った証明問題などを解説 遊ぶ数学

二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ

30 60 90 と 45 45 90 の直角三角形の辺の比 具体例で学ぶ数学

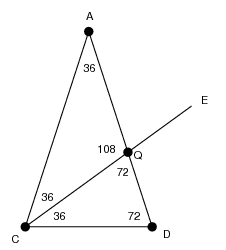
くろべえ 18 36 54 72 の三角比 Sin Cos

よく使う三角比の値 数学i By Okボーイ マナペディア

高校数学a 三角形の内角 外角の二等分線と辺の比の関係とその証明 受験の月

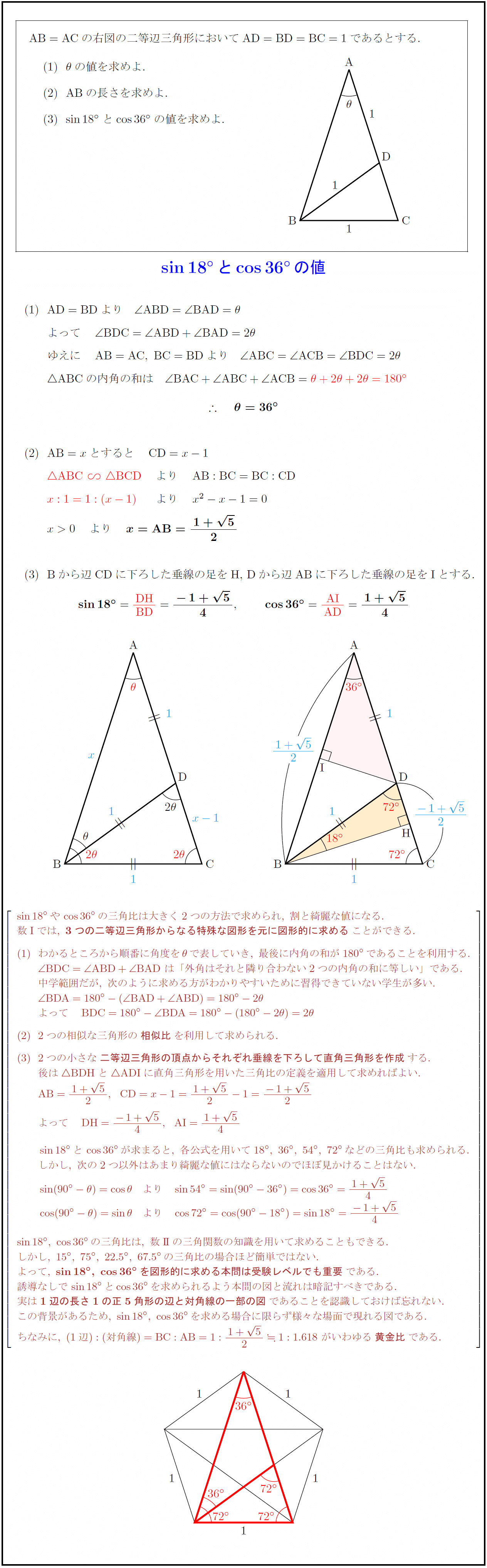
高校数学 Sin18 とcos36 の値 正五角形を利用した図形的解法 受験の月

中学数学 三平方の定理 特別な直角三角形 中学数学の無料オンライン学習サイトchu Su

三平方の定理 覚えること 三角定規 苦手な数学を簡単に

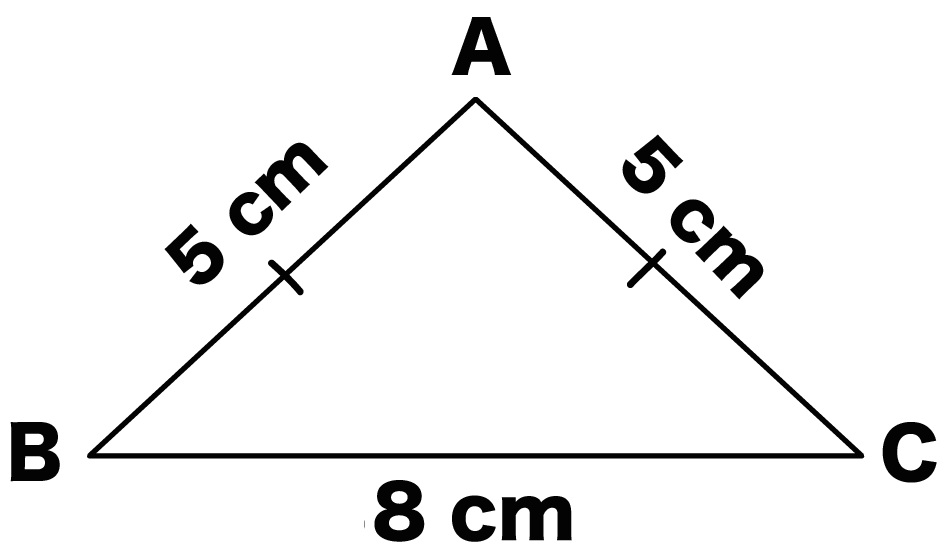
簡単計算 二等辺三角形の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

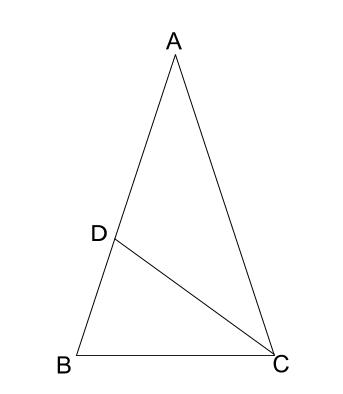
中学数学 相似と方程式 中学数学の無料オンライン学習サイトchu Su

直角二等辺三角形とは 定義や辺の長さの比 面積の求め方 受験辞典

二等辺三角形の分割

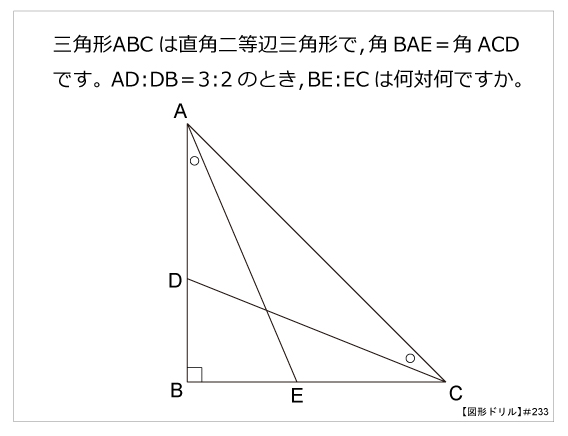
第233問 直角二等辺の辺の比 図形ドリル 第233問 直角二等辺の辺の比 算数星人のweb問題集 中学受験算数の問題に挑戦

二等辺三角形の底辺の長さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

3

応用 36度の三角比 なかけんの数学ノート

二等辺三角形の底辺は 1分でわかる意味 長さの計算 角度 高さ 三平方の定理との関係

中2数学 二等辺三角形の3大重要ポイント 映像授業のtry It トライイット

ラングレーの問題 整角四角形

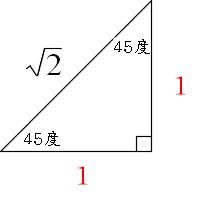
Mathematics 三平方の定理 ２ 特別な直角三角形 働きアリ

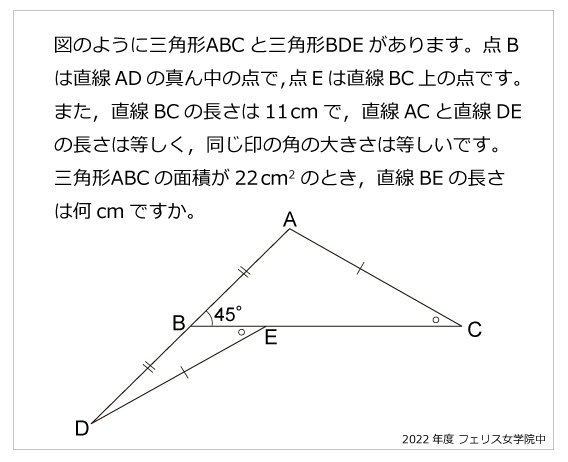
二等辺三角形 算数星人のweb問題集 中学受験算数の問題に挑戦

二等辺三角形の性質と辺の長さの求め方 押さえておきたい三辺の長さの比

各辺の比が決まっている三角形 中学数学 By Okボーイ マナペディア

テストによく出る直角三角形の辺の比 中学数学 By じょばんに マナペディア

スタディピア 図形

三角比 30 45 60 もう一度やり直しの算数 数学

Math Battle 0075 一辺を共有する二等辺三角形

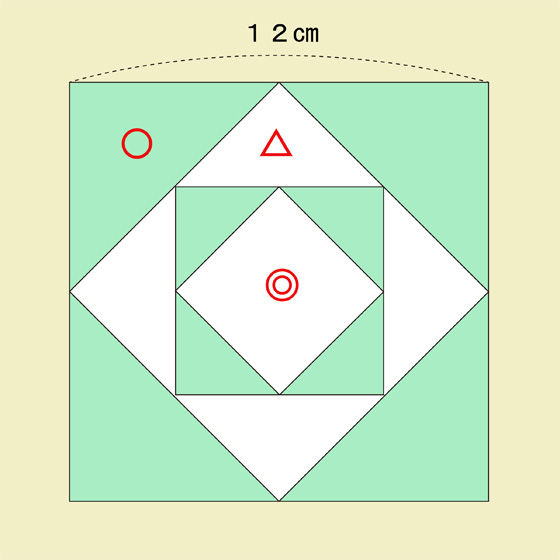
簡単に答えを出す方法に気付けるか 白い部分の面積を求める問題 秒刊sunday

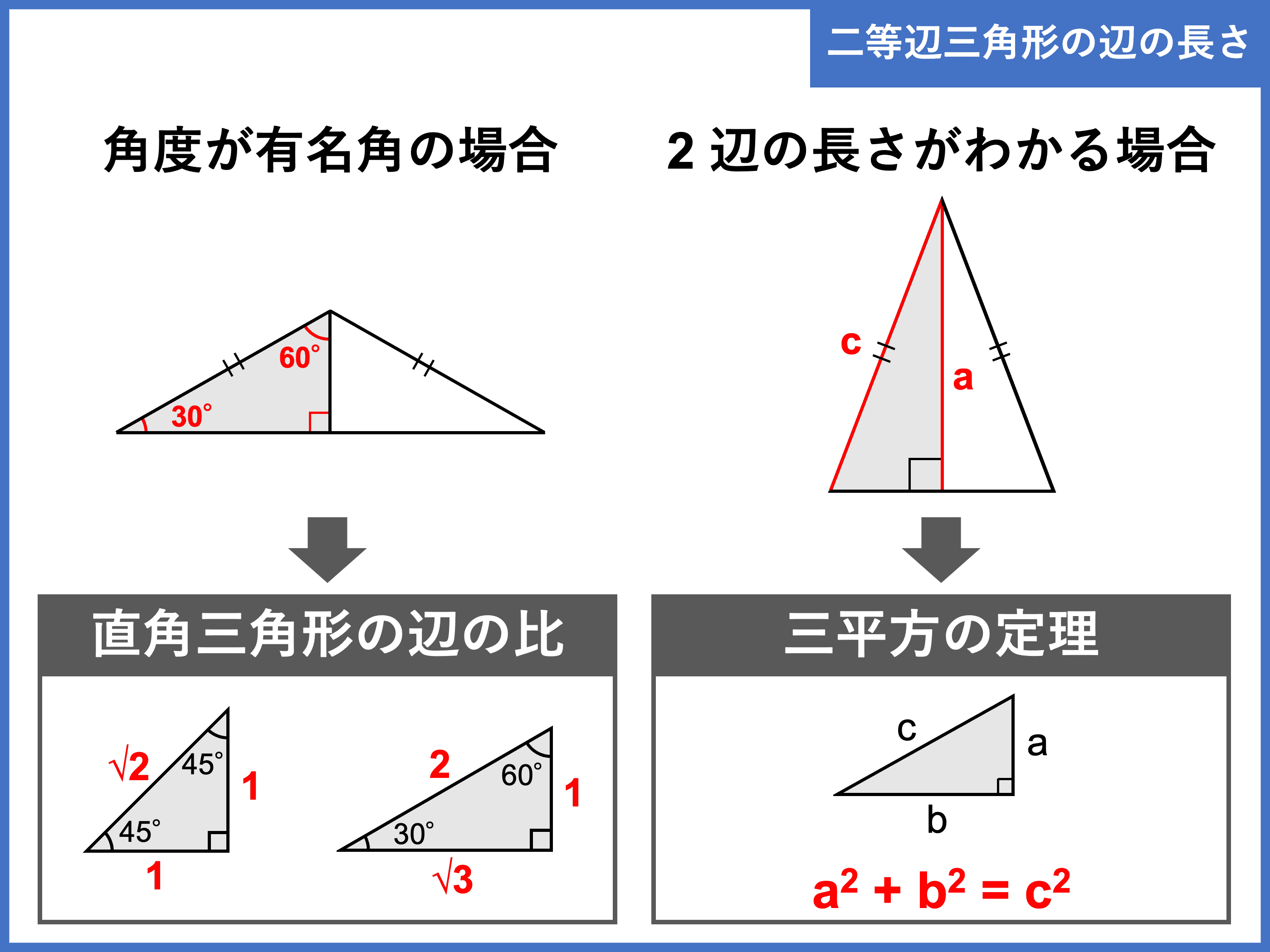
二等辺三角形とは 定義 定理や 角度 辺 面積の求め方 受験辞典

二等辺三角形であることの証明 二等辺三角形の定義性質 教遊者

二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ

直角二等辺三角形の辺の長さの求め方 具体例で学ぶ数学

高校入試 英語 数学 特別な直角三角形

数学の質問です ルート2はどこから分かるんですか 直角二等辺三角 Yahoo 知恵袋

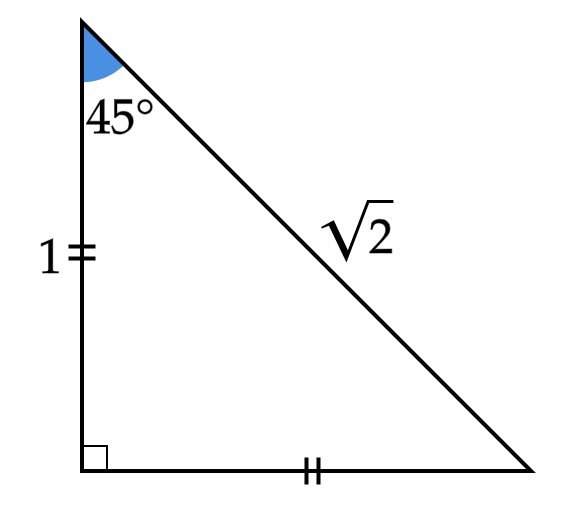
1つの辺の長さがわかれば面積が求められる特殊な三角形 数学について考えてみる

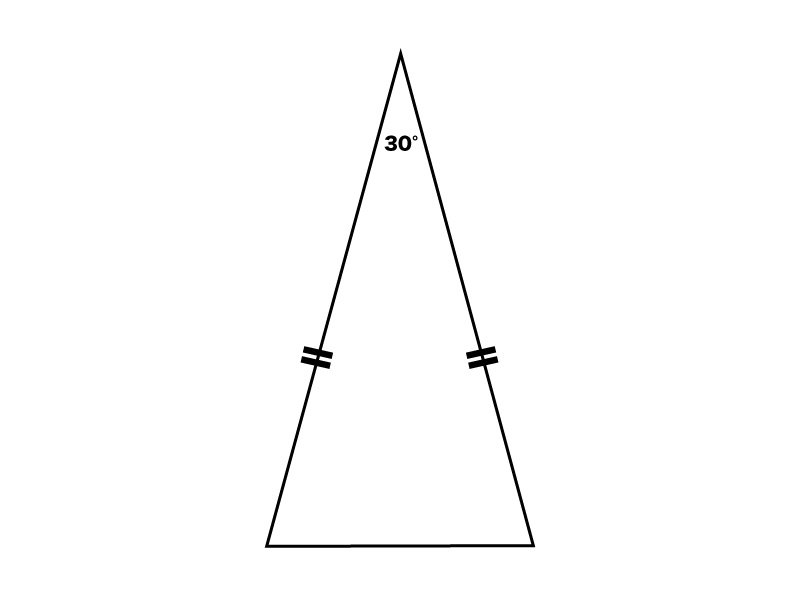
30 二等辺三角形の謎公式 斜辺 斜辺 4 って何 受験算数入門

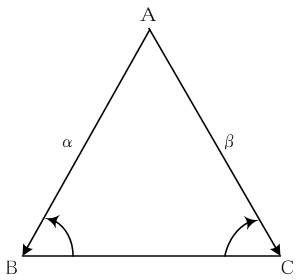
3 2 三角形とベクトル比

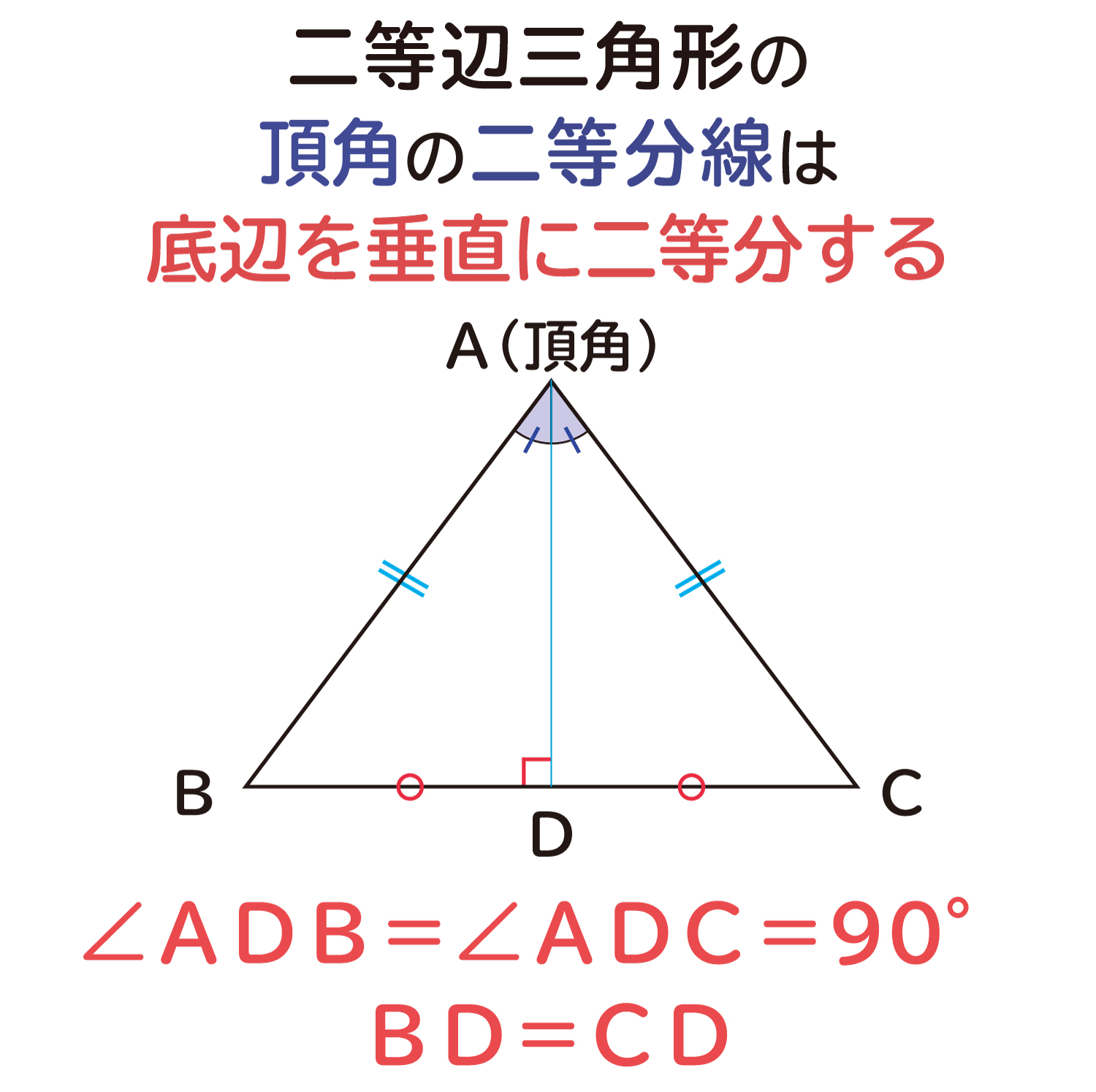
二等辺三角形の頂角の二等分線は 底辺を垂直に二等分する ことの説明 おかわりドリル

スタディピア 図形

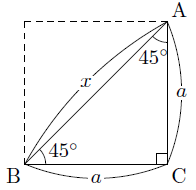
三角定規の3辺の比 まなびの学園

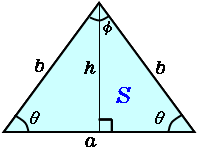
二等辺三角形 高精度計算サイト

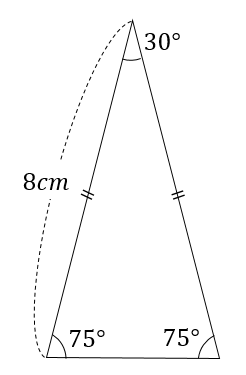
小学算数 30度の三角形ってどうやって面積求める 辺の比は 数スタ

頂角36度の二等辺三角形の辺の比を教えてください 頂角36度の二等辺三 数学 教えて Goo

白銀比三角形を見ていて気付いたこと 大したことない Yoshidanobuo S Diaryー高校数学の 思考 判断 表現力 を磨こう ー

Mathematics 三平方の定理 ３ いろいろな三角形 働きアリ

中2数学 二等辺三角形の3大重要ポイント 映像授業のtry It トライイット

二等辺三角形の底辺は 1分でわかる意味 長さの計算 角度 高さ 三平方の定理との関係

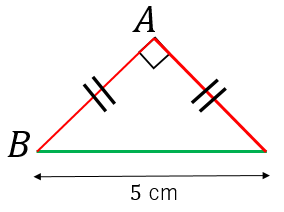
直角二等辺三角形の辺の長さの求め方 具体例で学ぶ数学

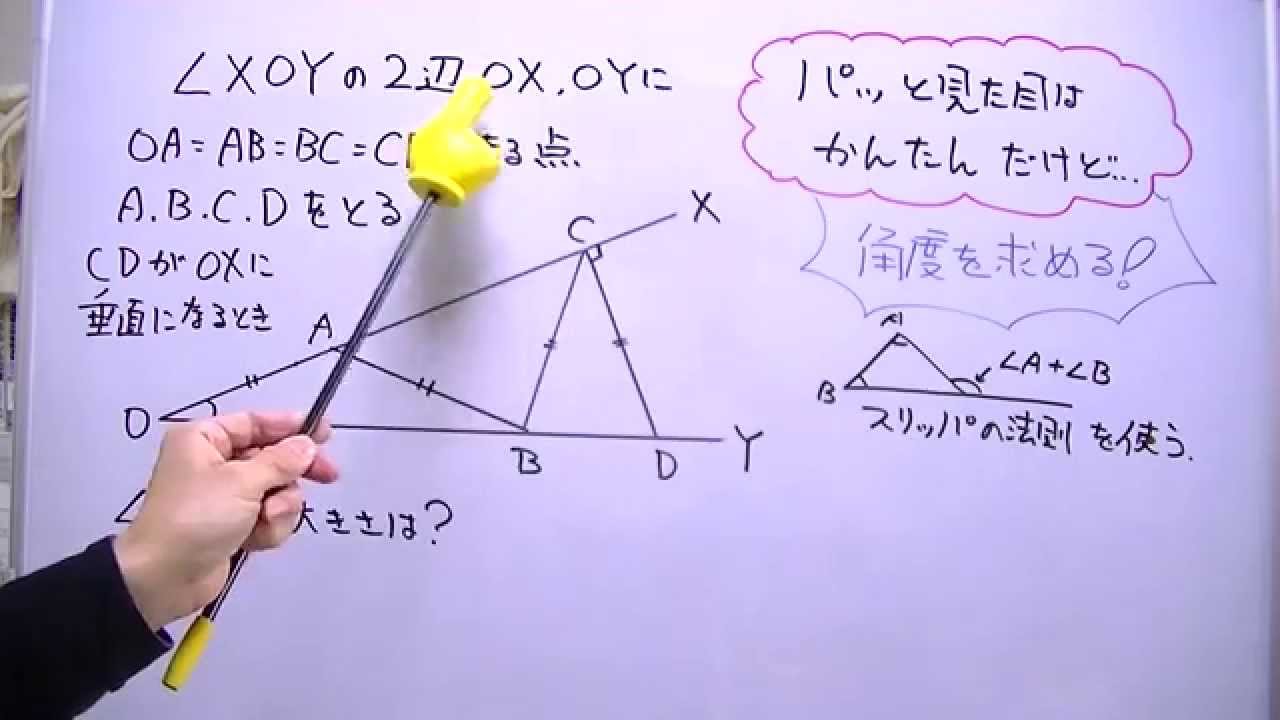
二等辺三角形とスリッパを組み合わせた角度問題 おときち副塾長 電脳空間学習塾かもん Youtube

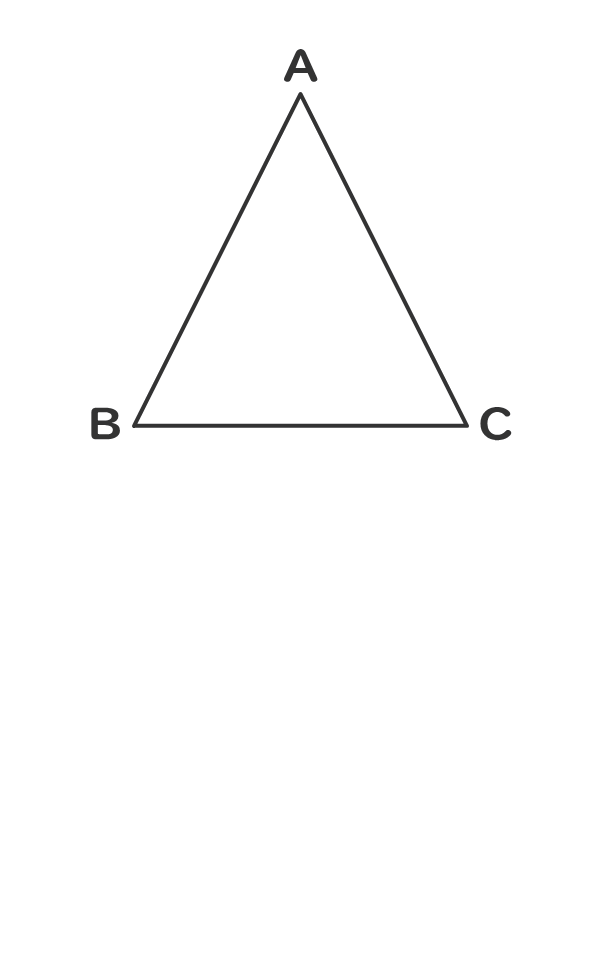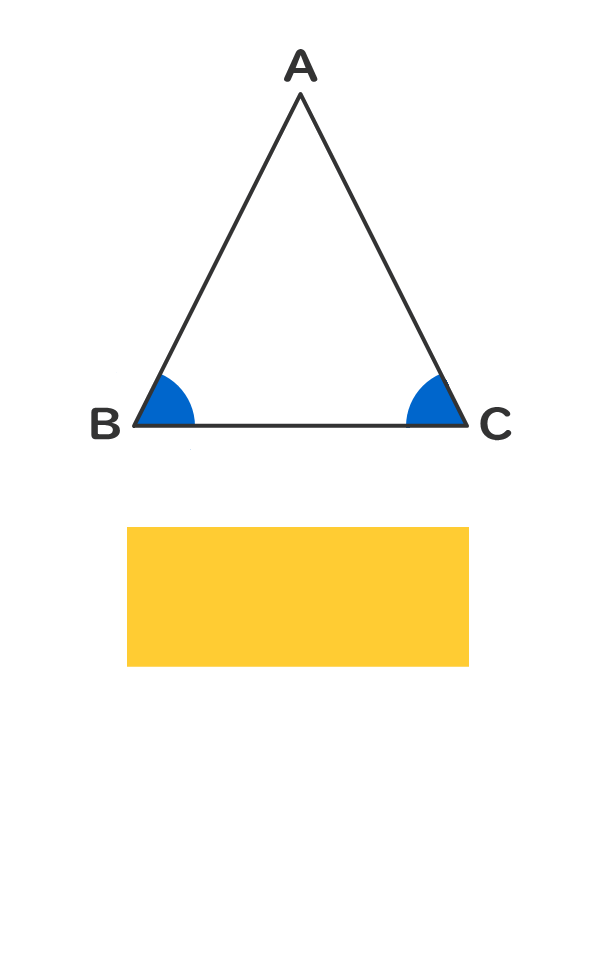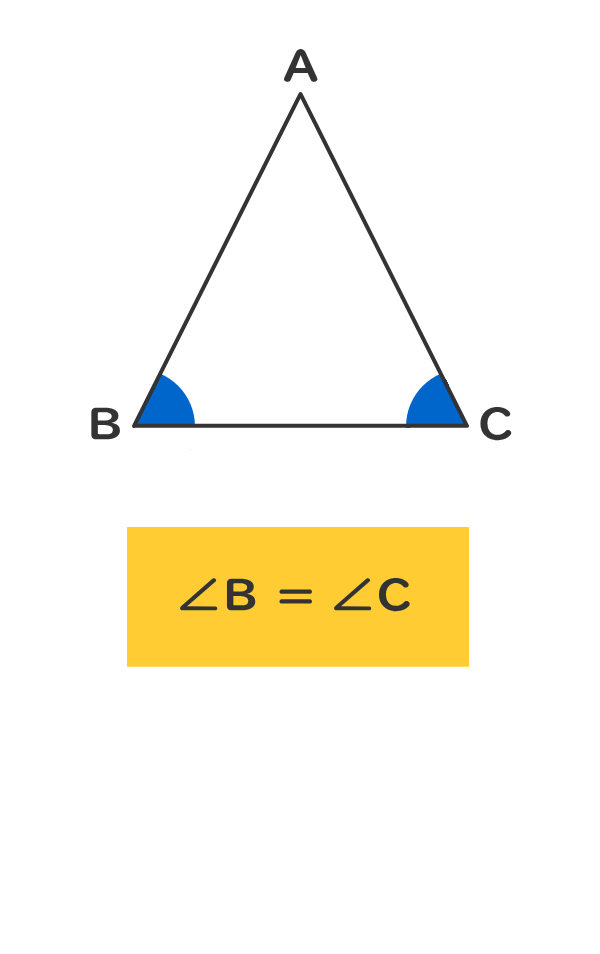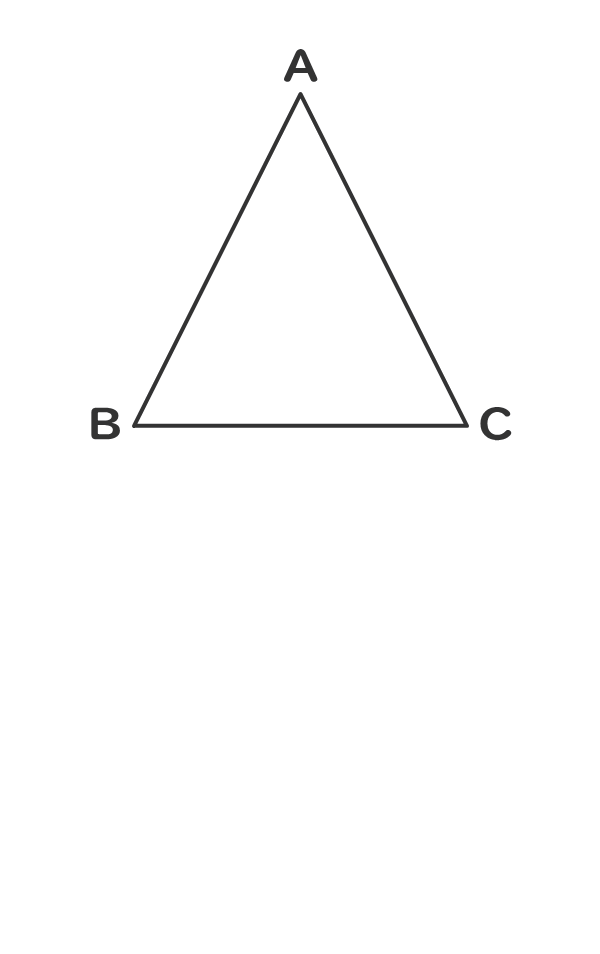
三角形の種類を判定しよう 電験3種web

二等辺三角形の各辺の比について質問です 二等辺三角形の Yahoo 知恵袋

直角二等辺三角形の辺の長さは 1分でわかる求め方 公式 辺の長さと角度の関係 証明

中高生必読 知らないとヤバい二等辺三角形の知識 定義 角度 面積 高校生向け受験応援メディア 受験のミカタ

Incoming Term: 二等辺三角形 辺の比,